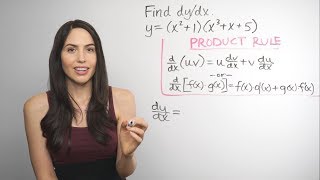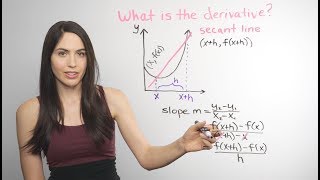MIT grad shows how to find the tangent line equation using a derivative (Calculus). To skip ahead: 1) For a BASIC example, skip to time 0:44. 2) For an example that uses the QUOTIENT RULE, skip to time 5:58. 3) For an example that uses TRIG FUNCTIONS and the CHAIN RULE for finding the equation of a tangent line, skip to time 11:35. Nancy formerly of MathBFF explains the steps.

For HOW TO FIND DERIVATIVES, jump to:    • Derivatives... How? (NancyPi)  

Follow me on Instagram!   / nancypi  
Follow me on Twitter:   / nancypi  

What is a tangent line? It is a line that is tangent to a curve at one point. You can use calculus for finding the tangent line equation, by taking the derivative of the given function.

Finding the EQUATION OF A TANGENT LINE using a DERIVATIVE:
There are four main steps to find the equation of a tangent line with derivatives:

1) TAKE DERIVATIVE: The first step is to take the derivative of the given equation, with respect to x. For instance, to find the equation of the line tangent to f(x) = x^2 + 3 at x = 4, first take the derivative of f(x), which is 2x, by the power rule.

2) PLUG IN X-VALUE INTO DERIVATIVE TO GET SLOPE: The second step is to plug the given x-value into the derivative of f(x). The value you get is the slope of the tangent line, m.

3) FIND Y-VALUE OF POINT WITH ORIGINAL EQUATION: The third step is to find the y-value of the point. You get this by plugging the given x-value into the original equation to find the corresponding y-value. Since you want the tangent line at x = 4, plug x = 4 into the original f(x), and you get a y-value of 7. Now that you have both the x and y coordinates, this means that the full point is (4,7).

4) PLUG THE SLOPE AND X,Y POINT VALUES INTO POINT-SLOPE EQUATION: The last step is to put the x and y point values, as well as the slope, m, into the point slope equation of a line. The point slope form is x - x1 = m (y - y1). Plug the x and y point values into this equation for x1 and y1. Plug the slope you found in for m. This is the equation of the tangent line. The equation will still have x and y variables in it.

You can also rearrange the equation you get so that it is in "y equals" or slope intercept form, if you want.

You may need to find the derivative with other derivative rules, such as the quotient rule or chain rule. Even if you need to use other rules when taking derivatives, or even if you need to differentiate something like a trigonometry function (ex. secant) or a fraction form with a numerator and denominator (rational function), the four main steps to find the equation of the tangent line will be the same.

For more math help, check out: http://nancypi.com